This essay is for the exhibition The Game of Life - Emergence in Generatiive Art, online at Kate Vass Gallery and is, in part, a tribute to the work of mathematician John Horton Conway, who passed away on April 11th, 2020, from COVID-19.
- Jason Bailey
For many people, it is hard to see the elegant connection that exists between art, math, and nature. Growing up, I loved studying art. I frequently sketched and painted from nature. However, I developed a math phobia early on and never saw what, for many, is the obvious thread between the worlds of art, math, and nature.
That changed when I started to write code in graduate school and learned about three new topics within a few weeks of each other:
These three interrelated discoveries completely changed my world view by showing me that much of the complexity we find in nature can be simulated and emulated using relatively basic algorithms.
This exhibition explores the idea of creating great complexity from deceptively simple algorithms or rule sets through the art of four generative artists: Alexander Reben, Manolo Gamboa Naon, Kjetil Golid, and Jared Tarbell. But before we jump into their art, let’s first define generative art, emergence, cellular automata, and the Game of Life.
Generative art is art that leverages a non-human, autonomous system which can help generate features in the artwork that would otherwise be left up to the artist to decide. In this exhibition, we are talking specifically about generative art written in computer code that includes elements of emergence or emergent behavior.
Emergence happens when two or more things come together to form something larger that has different properties than would be expected from the sum of the parts. Think of an ant colony. Each ant is pretty dumb, defenseless, and guided by very basic rules. But when combined with the many other ants in the colony, a new intelligence emerges at the colony level that allows them to adapt, defend themselves, and find food. The sophisticated emergent behavior of the colony cannot be predicted by understanding the limited capabilities of the individual ants. Flocks of birds and schools of fish operate in a similar manner, following a set of simple rules locally that result in complex behaviors globally. Emergence is not limited to our animal friends. Humans are a byproduct of emergent behavior, as is our economy, the weather, and traffic.
Artists, mathematicians, and computer scientists often generate their own complex emergent “ant colony-like” systems using a large grid of simple black and white squares called cellular automata. One of the most famous models of cellular automation is John Horton Conway’s Game of Life.
John Conway playing the Game of Life in 1974.
First published in the October, 1970 edition of Scientific American, the game is comprised of a grid of cells that, based on a few simple rules, either die or multiply, forming complex patterns. The rules are as follows:
Any live cell with fewer than two live neighbors dies, as if caused by underpopulation.
Any live cell with two or three live neighbors lives on to the next generation.
Any live cell with more than three live neighbors dies, as if by overpopulation.
Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
Through emergence, these very basic rules trigger surprisingly complex behaviors that can make a small set of black and white squares on a grid appear to "come to life."
Below is a example of the Game of Life I quickly programmed in Processing based on a tutorial by Daniel Shiffman.
After playing with the Game of Life, I and many others get a feeling that everything, no matter how complicated and mysterious it appears to be on the surface, may also be reducible to a basic set of algorithms. For artists, cellular automata like Game of Life can inspire them to improvise on these systems or to model emergent systems of their own, rivaling nature in their complexity, beauty, and surprise.
In his work puritan_communion, artist Alexander Reben plays with the rules of the Game of Life, cleverly programing in new rules that change the colors of the squares over time instead of using the traditional black and white color scheme. He explains:
In regular Game of Life, a cell can be either "alive" or "dead." In the case of the code, that means black or white. In this version, the colors are created by storing a history of the "world" wherein a new cell becomes yellow when "alive," and when that cell "dies," it changes color over time, eventually becoming black again.
The results remind me visually of a mix between a stop-motion video of flowers blooming in a garden and an intergalactic shootout between alien spaceships. Press the play button located underneath the image below to see the work unfold.

data:text/html,<!DOCTYPE html><!--9NM40_$2b$21$C//roHGH1lnglRcJzmDyTeOV8cJXv1Fm6UFsv.olqGBl8JJTxkWgG--><title>puritan_communion</title><style>*{width:100vmin;height:100vmin;margin:auto;position:absolute;top:0;bottom:0;left:0;right:0;background:black}</style><canvas id=A></canvas><script>S=10145920,A.width=A.height=W=2160,C=A.getContext`2d`,M=Math,R=_=>(S+=1831565813,m=M.imul(S^S>>>15,1|S),m=m+M.imul(m^m>>>7,61|m)^m,(m^m>>>14)>>>0)/2**32,C.globalCompositeOperation="copy",C.imageSmoothingEnabled=false,T=0,h=432,I=C.createImageData(h,h),g=Array.from({length:h},_=>Array.from({length:h},_=>0|2*R())),p=Array(h).fill().map(_=>Array(h)),s=0,F=t=>{if(T==-1||requestAnimationFrame(F),d=t-s,33<d){for(s=t-d% 33,T++,j=1;j<h-1;j++)for(k=1;k<h-1;k++){for(n=0,u=-1;2>u;u++)for(v=-1;2>v;v++)n+=g[j+u][k+v];n-=g[j][k],p[j][k]=0===g[j][k]?3==n?1:0:2==n||3==n?1:0}for(j=0;j<h;j++)for(k=0;k<h;k++)g[j][k]=p[j][k];for(j=0;j<h;j++)for(k=0;k<h;k++)i=4*(j+k*h),I.data[i+3]=h,r=i+1,u=I.data[r],v=I.data[i],g[j][k]?(I.data[r]=h,I.data[i]=h):8<u?I.data[r]=u-8:4<v?(I.data[i]=v-4,128>v&&(I.data[i+2]=h)):2<v&&(I.data[i+2]=v-2);C.putImageData(I,0,0),C.drawImage(A,0,0,h,h,0,0,W,W)}},F()</script>
You might think a work like puritan_communion would take a massive set of instructions since there are so many moving parts that go on for such a long time without ever repeating. That is the power of emergent behavior. The few short lines of code above actually capture all of the instructions needed to produce the entire animation. Try it yourself - simply copy the code above and paste it into your browser.
Boxie, Alexander Reben
Reben's background is in applied math and robotics, and his work is about the relationship between humanity and technology -- specifically, psychology and engineering. Reben's thesis at the MIT Media Lab focused on a robot he developed called Boxie. Boxie could only perform simple actions, but when you put all of those actions together, the robot appeared to be alive and intelligent. Boxie relates to Conway's Game of Life in that the actual programming and sensors required to make it appear alive were quite simple.
Obviously, neither Boxie nor the Game of Life are actually alive. However, there is something in our psychology that makes us think that they could be. As Reben explains:
Conway's Game of Life is more like half psychology and half math. We, as humans, are interpreting the actions of these pixels as having agency of some sort. We are picturing them as alive. Algorithms are only part of it. It is a human algorithm because it is our interpretation of what it is doing. I think that also plugs into viewing art. A lot of art is about how we interpret it in our own context. I bet a dog would interpret Conway's Game of Life differently than we do.
We will dive much deeper into Reben's fascinating work and share our full interview with the artist in the coming months. Let's take a look at how a second generative artist interprets Conway's Game of Life.
Argentine artist Manolo Gamboa Naon, better known as “Manolo,” is one of my favorite generative artists working today. He is a masterful colorist and a seemingly bottomless well of brilliant and engaging generative art. For his three interpretations of the Game of Life, Manolo layered several versions of the game playing out simultaneously, giving the illusion of depth and increasing its visual intricacy and dynamism. As Manolo explains:
I love when simple rules become really complex ... I feel that they even explain the world in a very reduced way. The videos that I made are several layers of Game of Life with different sizes. At first, I wanted to explore the patterns that remain static, live for a while, and reach a point where they do not mutate anymore ... and disappear with time, and new ones appear.
I made this work as a video because it seems that time is an essential element in the Game of Life. Initially, I thought to use Game of Life to find interesting images (there are aspects that remind me of a lot of pixel art -- I can't stop seeing characters from Space Invaders). But ultimately, I think "life" appears with movement/evolution/time. So I liked the idea of having two moments. First, they evolve and come alive, and then they die and disappear, and in time others are born, on and on like this forever.
The Game of Life is only one particular model of cellular automata. It is unique in that it is two dimensional and unfolds frame by frame over time, producing what looks like an animation. Unlike the Game of Life, one-dimensional (or elementary) cellular automata are designed based on rows.
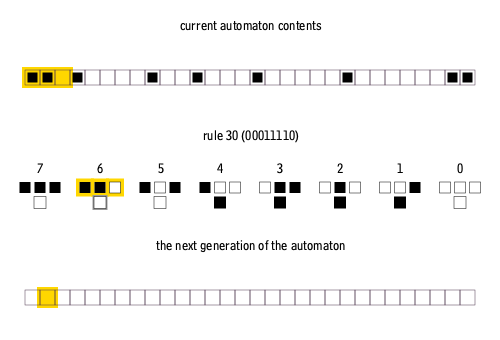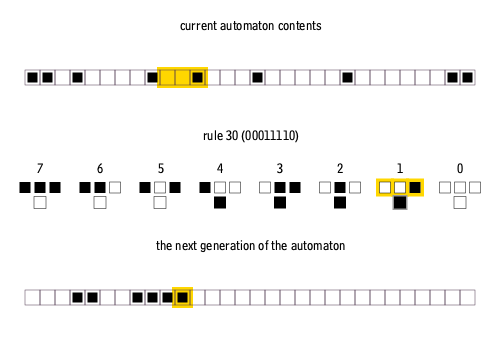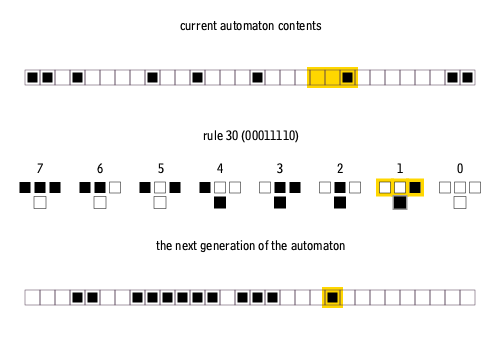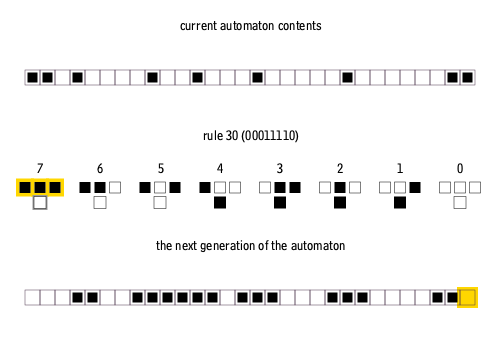
In elementary cellular automata, each cell still changes based on the "on/off" state of its neighbors. However, instead of eight neighbors, the cell changes based on just three cells: The cell to its upper left, the cell directly above, and the cell to its top right. The row below is then created based on whether those neighbors are on or off. This sequence repeats over and over again, row by row, quickly creating highly complex patterns from just those few rules. The animation below helps explain the rules and how the process unfolds.
An animation of the way the rules of a 1D cellular automaton determine the next generation.
- Cormullion CC BY-SA 4.0
There are a total of 256 possible rule combinations to create elementary cellular automata. Each rule has its own corresponding pattern (you can see all of them here) and a Wolfram number (named after mathematician Stephen Wolfram). Some automata are more famous than others for the beauty and complexity they produce when they are executed consecutively across a large number of rows, such as Rule #30.
Rule #30 Cellular Automation
Despite evolving from a basic formula, the markings produced by Rule #30 generate an intricate and labyrinthine non-repeating pattern. In this sense, it is similar to patterns we might find in nature. In fact, Rule #30 strongly resembles the patterns found on the shell of the venomous sea snail Conus textile.
A Textile Cone Snail (Conus textile) 2005. Photographer: Richard Ling richard@research.canon.com.au
I hope art lovers reading this who may have had less exposure to cellular automata, emergent systems, and generative art can start to see the connection between computational algorithms and the natural world. Computers, algorithms, and new technologies are not a threat to the natural beauty and humanity found in art (as I often hear from the traditional art world). In the skilled hands of generative artists, these tools actually strengthen our connection to the natural world and the systems that underpin it.
Kjetil Golid, a generative artist from Norway, has been developing a series of artworks inspired by one-dimensional cellular automata and noise fields. His process results in bold works with basket weave-like patterns that resemble graphic pixelated flags or banners. These works recall computing origins in the Jacquard loom, a device that employed punch cards to simplify the intricate weaving process of eighteenth-century textiles. Golid explains his process:
It's based on this traditional variant where pixels can be alive or dead on a 2D grid. I thought, ‘What if you don't change the rules, but instead, you change the visualization?’ Instead of using black and white pixels, I use lines that can go in different directions. While a 'standard' one-dimensional cellular automaton gets a pixel value from its three northern neighbors, this one is a hexagonal grid with lines in three directions. The existence of a specific line is dependent on the existence of its three 'preceding' lines. The lines split up the whole area into separate spaces, and I proceed to fill these spaces with colors. The colors are selected using a one-dimensional cellular automaton, with the color of each space being based on the left and upper neighboring spaces.
It turned out quite nice. It seems so random, but it is actually based on strict rules. The only seed for this randomness is the number you give it. So whenever you give it the number 120, you get exactly the same output. But it seems so random because it turns so complex so fast. The noise part comes from another piece I made, more of a tool really, that can distort any image.
In graduate school, Golid developed a fascination for structures and systems such as Turing machines, regular language, and deduction systems, all of which were the focus of his thesis. He found himself using programming to help himself understand and visualize these systems. However, it was actually at design school where he first started learning to program using the Processing programming language.
Not all generative art is inspired directly by cellular automata. Artists often develop their own emergent systems from scratch. Generative artist Jared Tarbell produced one of the better-known examples of this with his famous work Substrate in the early 2000s.
In a recent interview I conducted with Tarbell, he shared the inspiration behind this iconic and much-beloved work:
I was sitting in a coffee shop in Sante Fe, and there was this sticker in the window that was just blasted by the sun every day. It started to separate into these cracks, and I just saw the whole algorithm right there. Okay, there that first crack formed and got wider, and then another crack came off of it. I wrote the algorithm right there in the coffee shop. The desert sun is pretty brutal.
Tarbell was encouraged by his mother to make art in the home he grew in up quite a bit. However, his college studies focused on mathematics and computer science. He shared that while he viewed the world in a computational way, he wasn't afraid to express himself or try to find beauty in the computation.
Trying to understand and position ourselves within nature by understanding its algorithms and producing our own systems through the making of art can be a profoundly spiritual experience. I see Tarbell as a type of generative shaman unlocking new connections between us and the natural world around us -- and those connections are not always purely logical or fully explainable.
Shipibo Pattern , Jared Tarbell
One of Tarbell's recent works, Shipibo Pattern, is inspired by the patterns seen by Shipibo people, an indigenous tribe that lives in the Amazon rainforest in Peru. The Shipibo believe that there are distinctive patterns that act as healing forces (or destructive forces). As Tarbell explains:
During ceremony, a particular pattern is seen and heard by these people as a description of the reality of nature. I have seen it, too. The visual pattern is not what is actually witnessed, but an attempt to represent it in two dimensions. The patterns are composed of reflection, fractal self-similarity, and recursive motifs. Many of these constructions are native phenomena of computation. The Shipibo believe that the patterns are healing on emotional, physical, and spiritual levels. My personal experience with this vision leads me to believe it is an objective reality, one that can be modeled and explored.
Shipibo Pattern, Jared Tarbell
Tarbell shares the process he used to model this reality:
The background fuzz was generated with the common self-substituting Hilbert curve. Network connecting nodes were periodically added to points on the curve to allow more complexity.
The foreground object is fundamentally a maze of connected minos, reflected about both axes. Minos are adjacent collections of blocks. Two blocks can be called a domino, three blocks a trimino, four blocks a tetramino, and so on. This algorithm allows mino blocks up to 11.
A glow effect is achieved by placing multiple high alpha boxes of varying rotation and scale around each object. As with everything in generative art, the effect intensity is parameterized.
For me, emergence is evidence of a decentralized alternative to the more prevalent, centralized creation myth that dictates a sole divine architect created the world from some kind of rational blueprint. Instead, emergence and decentralization point towards an unlimited number of simpler entities following basic rules which come together to yield spectacular results. However, understanding the power of emergence and being spiritual are not mutually exclusive. As Tarbell shared in our interview:
I don't know if emergence describes everything. In fact, I kind of don't believe it does. I think there still are some very spiritual, mysterious elements to the universe. But certainly, thinking about problems computationally, you can get pretty far in understanding what's actually happening.
Magnifying and Exploring the Heart of the Buddhabrot, Jared Tarbell
Tarbell, like myself, grew up in the Mormon faith. We are both no longer active members of the church. However, we both grew up deeply invested in trying to live a spiritual life, and we both ultimately struggled to reconcile math, science, and logic with our religious upbringing. In some ways, I think this struggle has made us both seekers, ultimately leading us to the world of generative art. That strong desire to understand our place in the world and the connectivity between all that there is does not just go away when you stop going to church. For us, creating generative art and exploring emergence offers a spiritual path towards better understanding the “game of life” in which we all participate.
Some Final Thoughts
It's been a difficult year for people all around the world. Most of us have had to isolate ourselves from our friends and families to help prevent the spread of the COVID-19. Art can seem trivial in times like this, but I believe this is when we need art more than ever. I chose to create this exhibition with the hope that it can play a small role in helping us better understand the healing patterns hidden in nature, which some artists (like those in this exhibition) regularly unlock to unite us all at a time when we really need it.
Sincere thanks to the Kate Vass Galerie for sponsoring the curation of this exhibition. To inquire about the artists in this exhibition and to see more of their works, visit Kate Vass Galerie. I am sincerely grateful to the artists who trusted me to write about their work and share it with the world.